Integrating 2D electric field lines with SciPy
In previous chapters I’ve describe how to plot continuous electric field lines with with Matplotlib and with Mayavi. The main disadvantage of these methods, it that you almost have no control over these lines, receiving some kind of final picture. And matplotlib do not give continuous lines in 3D space. In this tutorial we will use SciPy module to calculate these lines by data given only on the meshgrid.
NOTE! It is important to understand, that 2D case is not natural case and for electric field lines it is important calculate 3D space, but this tasks is good for understanding how to integrate this kind of vector fields.
Preparation for E-field line calculation
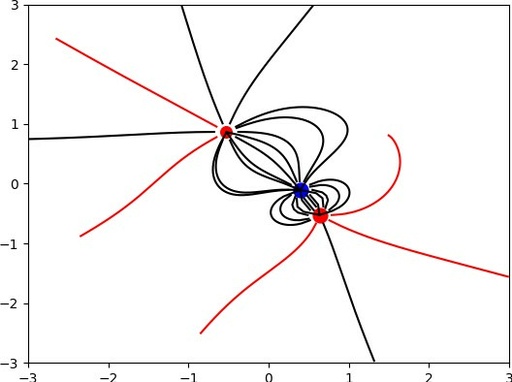
Electric field lines integrated with ODE. Red lines – are lines with required more steps for integrating. Also you can see that the lines are not always stopped at the edge of charge rings. Lines are not evenly distributed in the space, but it is separate very complicated task to make them evenly distributed.
Original image: 528 x 394
Libraries
For these calculations we need to load NumPy and Matplotlib as a standard. And also we need to load RegularGridInterpolator from SciPy for interpolation of our grid data to continuous domain, and finally ode from SciPy for integration of our vector data.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import ode
from scipy.interpolate import RegularGridInterpolator as RGIDefining domain parameters.
At this step we will define all necessary domain parameters and will also calculate Electric Field on the given mesh-grid. This simple task was described in this tutorial.
So briefly, we need to have domain parameters. We will use domain from -3 to 3 in X and Y dimensions with the step of 0.01. The coordinates grid I will do with mgrid function.
NQ=3 charges we will randomly place in the area from -1 to 1. This difference is important to have trace of the electric field lines beyond the charge box.
Then we initialize empty arrays for electric field, by multiplying our coordinate grid by 0 and then calculate electric field in every point.
At the last step I will make linear approximation of out electric field within the domain, as it is described here.
# Defining domain parameters
s, e, d = -3, 3, 0.01
X, Y = np.mgrid[s:e:d, s:e:d]
NQ = 3
Q = np.random.uniform(low=-1, high=1, size=(NQ,3)) # x, y, charge
Ex = 0*X
Ey = 0*Y
# Random placing charges
for q in Q:
r2 = (X - q[0])**2 + (Y - q[1])**2
Ex += q[2]*(X - q[0]) / r2**(3/2)
Ey += q[2]*(Y - q[1]) / r2**(3/2)
Exi = RGI((X[:, 0], Y[0, :]), Ex, method='linear')
Eyi = RGI((X[:, 0], Y[0, :]), Ey, method='linear')Electric field line integration parameters.
For integration of our electric field lines, we need to specify integration model. In ode from SciPy you can use the following models:
- vode - Real-valued Variable-coefficient Ordinary Differential Equation solver, with fixed-leading-coefficient implementation. It provides implicit Adams method (for non-stiff problems) and a method based on backward differentiation formulas (BDF) (for stiff problems).
- lsoda - Real-valued Variable-coefficient Ordinary Differential Equation solver, with fixed-leading-coefficient implementation. It provides automatic method switching between implicit Adams method (for non-stiff problems) and a method based on backward differentiation formulas (BDF) (for stiff problems).
- dopri5 - This is an explicit runge-kutta method of order (4)5
- dop853- This is an explicit runge-kutta method of order 8(5,3)
Then it is necessary to limit maximal number of integration steps – to avoid cyclical and endless solutions (2000), give minimal integration step (0.01).
Next, it is necessary to give start points for electric line calculations and endpoints. Around every charge we will make a circle of radius 0.15 and uniformly distribute 10 start points on it. The end of the line will be at the border of the domain, or when it will approach to other charge to a close distance (less than radius).
Also here I will create function Intergrate_Line with take integration time (default but not used parameter here) and coordinates and return the Field value for the given point. This function will be used by ode integrator. If the function will fails to find the electric field values (out of the domain, or near the border), then it will reset abort switch.
When everything is ready – initialize space for plotting image
# defining integration model
integrmodel = 'vode' # 'lsoda', 'dopri5', 'dop853'
max_step = 2000
step_size = 0.01
n_sphere = 10
Rsphere = 0.15
Rsphere2 = Rsphere ** 2
def Intergrate_Line(t, coord):
# Function calculating Efield in every point for integrator
global abort
xi = coord[0]
yi = coord[1]
try:
ex = Exi([xi, yi])[0]
ey = Eyi([xi, yi])[0]
except:
abort = True
return [False, False]
return [ex, ey]
fig, ax = plt.subplots()Integrating procedure
Now I will calculate electric lines itself. I will do cycle for every charge. In every cycle I will set up initial step from the default value and then if the charge is negative – will use it with opposite sign, to calculate this line in different direction.
Then for charge I will create uniformly distributed start dots around every charge. It is easy to do in 2D space with linspace function. It is also possible to place these dots randomly – for some tasks it give better line distribution.
Then for every angle I will calculate it relative electric field line with the following steps: set up function for integrator, then specify integration model used for calculation.
After I will set up initial spot lx and ly around the sphere in according with the given angle and give these values ti the integrator set_initial_value with 0 time (it is dummy parameter not used here)
Then I do reset my step counted and reset the abort status.
After this, I will run integration until it returns successful status with cycle while. On every step I do update my step counter, integrate coordinates for the given step, and check the coordinates. If the coordinates are not False, then I do add them to my list with this line coordinates and check, that they are not within the allowed radius from any charger. If yes, then I do abort calculations.
If my last point are out of the domain area, then I do abort this line calculation. If I do exceed maximal number of steps I do about calculation as well.
And now I do plot this line. If it is aborted due to number of integration steps, then I do plot it with the red colour, otherwise it will be black.
for q in Q:
dt = step_size
if q[2] < 0:
dt *= -1
for angle in np.linspace(0, 2*np.pi*(n_sphere-1)/n_sphere, n_sphere):
#ANG = np.random.uniform(low=0, high=2*np.pi, size=(n_sphere))
#for angle in ANG:
# set up function for integrator
r = ode(Intergrate_Line)
r.set_integrator(integrmodel)
lx = [q[0] + np.cos(angle) * Rsphere]
ly = [q[1] + np.sin(angle) * Rsphere]
r.set_initial_value([lx[0], ly[0]], 0)
step = 0
abort = False
while r.successful():
step += 1
r.integrate(r.t+dt)
x, y = r.y[0], r.y[1]
if x is False:
abort = True
else:
lx.append(x)
ly.append(y)
for qf in Q:
if (x - qf[0])**2 + (y - qf[1])**2 < Rsphere2:
abort = True
if abort is True:
break
if s >= x or e <= x or s >= y or e <= y or \
step >= max_step:
break
if step >= max_step:
plt.plot(lx, ly, 'r')
else:
plt.plot(lx, ly, 'k')Final drawings
At the next step I do draw big circles for charges. Blue for negative charge and red for positive (in video I do mix them)
Then I do set the lomits for the plotting domain and that it. Job done.
for q in Q:
if q[2] < 0:
plt.scatter(q[0], q[1], s=abs(q[2])*200, color='b')
else:
plt.scatter(q[0], q[1], s=abs(q[2])*200, color='r')
ax.set_xlim(s, e)
ax.set_ylim(s, e)
plt.show()If you have some question, please watch our video:
Share it, subscrive to the channel and comment there
Full code:
Finally you can find the full working code for integrating electric field lines on the domain from few point charges here:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import ode
from scipy.interpolate import RegularGridInterpolator as RGI
# Defining domain parameters
s, e, d = -3, 3, 0.01
X, Y = np.mgrid[s:e:d, s:e:d]
NQ = 3
Q = np.random.uniform(low=-1, high=1, size=(NQ,3)) # x, y, charge
Ex = 0*X
Ey = 0*Y
# Random placing charges
for q in Q:
r2 = (X - q[0])**2 + (Y - q[1])**2
Ex += q[2]*(X - q[0]) / r2**(3/2)
Ey += q[2]*(Y - q[1]) / r2**(3/2)
Exi = RGI((X[:, 0], Y[0, :]), Ex, method='linear')
Eyi = RGI((X[:, 0], Y[0, :]), Ey, method='linear')
# defining integration model
integrmodel = 'vode' # 'lsoda', 'dopri5', 'dop853'
max_step = 2000
step_size = 0.01
n_sphere = 10
Rsphere = 0.15
Rsphere2 = Rsphere ** 2
def Intergrate_Line(t, coord):
# Function calculating Efield in every point for integrator
global abort
xi = coord[0]
yi = coord[1]
try:
ex = Exi([xi, yi])[0]
ey = Eyi([xi, yi])[0]
except:
abort = True
return [False, False]
return [ex, ey]
fig, ax = plt.subplots()
for q in Q:
dt = step_size
if q[2] < 0:
dt *= -1
for angle in np.linspace(0, 2*np.pi*(n_sphere-1)/n_sphere, n_sphere):
#ANG = np.random.uniform(low=0, high=2*np.pi, size=(n_sphere))
#for angle in ANG:
# set up function for integrator
r = ode(Intergrate_Line)
r.set_integrator(integrmodel)
lx = [q[0] + np.cos(angle) * Rsphere]
ly = [q[1] + np.sin(angle) * Rsphere]
r.set_initial_value([lx[0], ly[0]], 0)
step = 0
abort = False
while r.successful():
step += 1
r.integrate(r.t+dt)
x, y = r.y[0], r.y[1]
if x is False:
abort = True
else:
lx.append(x)
ly.append(y)
for qf in Q:
if (x - qf[0])**2 + (y - qf[1])**2 < Rsphere2:
abort = True
if abort is True:
break
if s >= x or e <= x or s >= y or e <= y or \
step >= max_step:
break
if step >= max_step:
plt.plot(lx, ly, 'r')
else:
plt.plot(lx, ly, 'k')
for q in Q:
if q[2] < 0:
plt.scatter(q[0], q[1], s=abs(q[2])*200, color='b')
else:
plt.scatter(q[0], q[1], s=abs(q[2])*200, color='r')
ax.set_xlim(s, e)
ax.set_ylim(s, e)
plt.show()
Published: 2022-11-21 22:42:05