Electric field potential and intensity due to point charges
In this article I will show, how to calculate and visualise with Python Electric field potential and intensity due to point charges. For these calculations I will use Numpy and Matplotlib.
Initializing domain for calculations
For displaying electric field intensity and potential in some area (we call it domain) it is necessary to calculate it in every point of this domain. Usually, domain is slitted into a mesh of cells and this value calculated for every cell.
import numpy as np
import matplotlib.pyplot as plt
xrange = [-1., 1.]
step = 100
qrange = [-10., 10.]
NQ = 5
xlist = np.linspace(xrange[0], xrange[1], step)
ylist = np.linspace(xrange[0], xrange[1], step)
X, Y = np.meshgrid(xlist, ylist)
qmin = [xrange[0], xrange[0], qrange[0]]
qmax = [xrange[1], xrange[1], qrange[1]]
q = np.random.uniform(low=qmin, high=qmax, size=(NQ,3))
Ex = np.zeros_like(X)
Ey = np.zeros_like(Y)
V = np.zeros_like(X)I will use squared 2-dimensional domain, therefore range in x and y axes will be the same. I ill use range from -1 to 1 with 100 steps, and I will generate randomly 5 (NQ) charges with charge from -10 to 10.
This is all x values xlist = np.linspace(xrange[0], xrange[1], step) and the same for ylist. At the next step I will create domain for X and Y with function np.meshgrid. This will create domains X and Y and fill every cell of this domain with values of x and y in these cells respectively. From on hand it can looks a bit excessive and overloading of repetitive information, but it will make all numpy matrix calculations much easier.
Then we need to create random list of charges as a numpy array for example, and we can do it with np.random.uniform with providing list of minimal and maximal values and in size specify the size of this array.
At the last step – create numpy arrays for Ex, Ey and V (X and Y component of Electric intensity and Electric potential), filled with 0. Because these array will represent our domain, we can just make a similar arrays like out X or Y arrays with function np.zeros_like
Calculation of Electric field potential and intensity
Electric field potential and Electric field intensity in stationary case are linear and it is possible to calculate it for every charge and then add them together. This will make all calculations much easier. Also electric field intensity is a vector value and we van calculate X and Y component according to the basis of our domain.
def addPointCharge2D(V, Ex, Ey, X, Y, q):
# q[0] – x coordinate of the charge
# q[1] – y coordinate of the charge
# q[2] – charge value
r2 = (X - q[0])**2 + (Y - q[1])**2
Ex += q[2]*(X - q[0])/r2**(3/2) # Electric field (x)
Ey += q[2]*(Y - q[1])/r2**(3/2) # Electric field (y)
V += q[2]/r2**0.5
return V, Ex, Ey
for i in range(NQ):
addPointCharge2D(V, Ex, Ey, X, Y, q[i])
E = np.log((Ex**2 + Ey**2)**0.5)At the beginning, we calculating the distance matrix in every point to the charge given, but we are calculating distance squared. It doesn’t matter, because later we will take square rood of it. For performance optimisation, it is important to do not make the same operation few times, and we can optimize it by calculating distance cubed first and then take cubic root for electric potential calculations. We will reduce one power operation but the code will be a bit more complicated.
And finally, we do not need to return calculated values, because we working with references and the original data will be updated anyway, but I will return them just in case.
At the last step It is necessary to calculate absolute value of electric field intensity and to make it more easy to visualize, take a log of it.
Visualisation
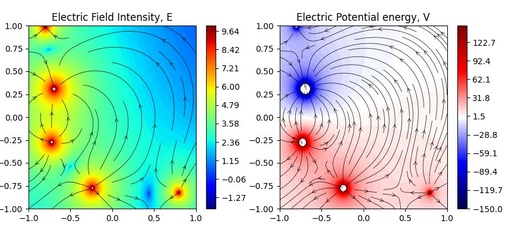
Electric field intensity (left) and Electric potential energy (right) generated by five point charges. Electric field lines with different display density are shown on both pictures.
Original image: 862 x 387
Electric field lines
Last step is visualisation.
Because we will join few graphs on the same plot, we need to use axes. First of all we can plot electric field intensity as electric field lines with streamplot function.
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(121)
ax.set_title("Electric Field Intensity, E")
ax.streamplot(X, Y, Ex, Ey, color='black', linewidth=0.5,
density=0.5, arrowstyle='->', arrowsize=1.0)So, we’ve create figure to make two plots with mentioning size in inches. Then we’ve create axes for first subplot at the position 1 (121) in the field with height=1 and width=2.
Then we make a title for this plot and finally draw lines with streamplot, using X and Y coordinates, with Ex, Ey values and define some parameters of these lines.
Contour line map
For plotting contour map we need to define levels for plotting. Use np.linespace to define all levels. Despite electric field intensity is always positive, the way of plotting these contour map can approximate it to negative values, so it is better to start make levels from negative value. Secondly, because the step of domain can leat do different accuracy of calculations, we need to limit top value to a pretty reasonable value.
Very high accuracy can give unlimitedly high value near the point charge and in our linear layer distribution, all layers will be concentrated around charge, So it is better to restrict it.
levels = np.linspace(-2, 10, 100)
cp = ax.contourf(X, Y, E, levels=levels, cmap='jet')
fig.colorbar(cp)Also it is necessary to chose nice colour-map. For values from 0 to high values, I do advise to use cmap='jet'. For values from negative to positive values, I do advise to use cmap='seismic' colour scheme.
The same we will do for the electric potential energy map.
Final code
import numpy as np
import matplotlib.pyplot as plt
def addPointCharge2D(V, Ex, Ey, X, Y, q):
r2 = (X - q[0])**2 + (Y - q[1])**2
Ex += q[2]*(X - q[0])/r2**(3/2) # Electric field (x)
Ey += q[2]*(Y - q[1])/r2**(3/2) # Electric field (y)
V += q[2]/r2**0.5
return V, Ex, Ey
xrange = [-1., 1.]
step = 100
qrange = [-10., 10.]
NQ = 5
xlist = np.linspace(xrange[0], xrange[1], step)
ylist = np.linspace(xrange[0], xrange[1], step)
X, Y = np.meshgrid(xlist, ylist)
qmin = [xrange[0], xrange[0], qrange[0]]
qmax = [xrange[1], xrange[1], qrange[1]]
q = np.random.uniform(low=qmin, high=qmax, size=(NQ,3))
Ex = np.zeros_like(X)
Ey = np.zeros_like(Y)
V = np.zeros_like(X)
for i in range(NQ):
addPointCharge2D(V, Ex, Ey, X, Y, q[i])
E = np.log((Ex**2 + Ey**2)**0.5)
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(121)
ax.set_title("Electric Field Intensity, E")
ax.streamplot(X, Y, Ex, Ey, color='black', linewidth=0.5,
density=0.5, arrowstyle='->', arrowsize=1.0)
levels = np.linspace(-2, 10, 100)
cp = ax.contourf(X, Y, E, levels=levels, cmap='jet')
fig.colorbar(cp)
ax = fig.add_subplot(122)
ax.set_title("Electric Potential energy, V")
ax.streamplot(X, Y, Ex, Ey, color='black', linewidth=0.5,
density=1.0, arrowstyle='->', arrowsize=1.0)
levels = np.linspace(-150, 150, 100)
cp = ax.contourf(X, Y, V, levels=levels, cmap='seismic')
fig.colorbar(cp)
plt.show()
Published: 2022-09-18 23:27:50
Updated: 2022-09-18 23:29:16