Integrating 3D electric field lines with SciPy
In the previous chapters I’ve describe how to calculate and plot Electric Field Lines for 2 dimensional case with ODE from SciPy. In this tutorial I will show, how you can easily swat these calculations to the 3D case.
NOTE! It is important to understand, that 3D case will use seriously more computer memory and will be much slower as well. Therefore, please pay attention for selection of the domain and grid sizes.
Essential modification from 2D to 3D conversion
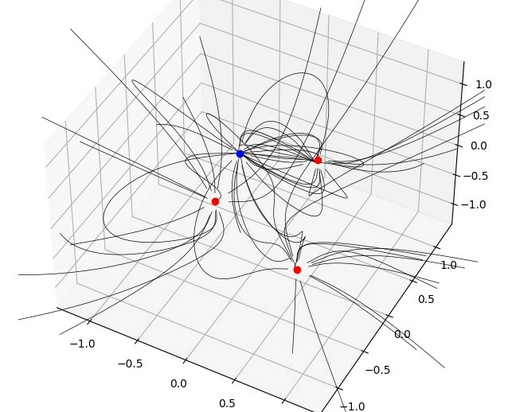
3D Electric Field lines integrated with ODE from SciPy
Original image: 643 x 518
Previously, all starting points were evenly distributed around point charge in the 2D space. In 3D space it is pretty difficult evenly distribute starting points around the charge. It is very difficult mathematical task about even distributing objects on the sphere. Therefore I will place these starting point randomly.
In total we will take 15 points around each sphere. Also domain will be smaller – from -2 to 2 and step-size will be 0.05. I will place 4 random charges and will make all charges +1 or -1. Again, physically, charges will be located in the space from -1 to +1
Charge now will have 4 parameters, x, y, z and q
n_sphere = 15
s, e, d = -2, 2, 0.05
X, Y, Z = np.mgrid[s:e:d, s:e:d, s:e:d]
NQ = 4
Q = np.random.uniform(low=-1, high=1, size=(NQ,4))
Q[:,3] /= np.abs(Q[:,3]) # make charge +1 or -1Electric field will be calculated for 3 dimensions. And respectively, it should be interpolated on 3D grid as well
Ex = 0*X
Ey = 0*Y
Ez = 0*Z
for q in Q:
r2 = (X - q[0])**2 + (Y - q[1])**2 + (Z - q[2])**2
Ex += q[3]*(X - q[0]) / r2**(3/2)
Ey += q[3]*(Y - q[1]) / r2**(3/2)
Ez += q[3]*(Z - q[2]) / r2**(3/2)
Exi = RGI((X[:, 0, 0], Y[0, :, 0], Z[0, 0, :]), Ex, method='linear')
Eyi = RGI((X[:, 0, 0], Y[0, :, 0], Z[0, 0, :]), Ey, method='linear')
Ezi = RGI((X[:, 0, 0], Y[0, :, 0], Z[0, 0, :]), Ez, method='linear')Interpolation function should work in 3D space as well
def IL3(t, coord):
global abort
xi = coord[0]
yi = coord[1]
zi = coord[2]
try:
ex = Exi([xi, yi, zi])[0]
ey = Eyi([xi, yi, zi])[0]
ez = Ezi([xi, yi, zi])[0]
except:
abort = True
return [0, 0, 0]
return [ex, ey, ez]Starting points for electric field lines
It is very difficult to distribute evenly objects on the sphere and this is not a goal for this lesson. Therefore I will do simplest distribution of the starting points on the sphere – random distribution.
I will Do select randomly angled PHI and TETA and then use them as a random spherical coordinated for the starting points.
See how to convert spherical coordinated to orthogonal system:
for i in range(n_sphere):
phi = random.uniform(-np.pi, np.pi)
tet = random.uniform(-np.pi, np.pi)
lx = [q[0] + np.sin(phi) * np.cos(tet) * Rsphere]
ly = [q[1] + np.sin(phi) * np.sin(tet) * Rsphere]
lz = [q[2] + np.cos(phi) * Rsphere]That it. Everything is converted, The minor leftovers, how to build 3D plot – you can find in the video about 3D electric Field Lines, or check the full working script below.
Full script
The procedure of making this script is described in the video below:
or see the full script here:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import ode
from scipy.interpolate import RegularGridInterpolator as RGI
import random
integrmodel = 'vode' # 'lsoda', 'dopri5', 'dop853'
max_step = 2000
step_size = 0.01
n_sphere = 15
Rsphere = 0.15
s, e, d = -2, 2, 0.05
Rsphere2 = Rsphere ** 2
X, Y, Z = np.mgrid[s:e:d, s:e:d, s:e:d]
NQ = 4
Q = np.random.uniform(low=-1, high=1, size=(NQ,4))
Q[:,3] /= np.abs(Q[:,3])
Ex = 0*X
Ey = 0*Y
Ez = 0*Z
for q in Q:
r2 = (X - q[0])**2 + (Y - q[1])**2 + (Z - q[2])**2
Ex += q[3]*(X - q[0]) / r2**(3/2)
Ey += q[3]*(Y - q[1]) / r2**(3/2)
Ez += q[3]*(Z - q[2]) / r2**(3/2)
Exi = RGI((X[:, 0, 0], Y[0, :, 0], Z[0, 0, :]), Ex, method='linear')
Eyi = RGI((X[:, 0, 0], Y[0, :, 0], Z[0, 0, :]), Ey, method='linear')
Ezi = RGI((X[:, 0, 0], Y[0, :, 0], Z[0, 0, :]), Ez, method='linear')
def IL3(t, coord):
global abort
xi = coord[0]
yi = coord[1]
zi = coord[2]
try:
ex = Exi([xi, yi, zi])[0]
ey = Eyi([xi, yi, zi])[0]
ez = Ezi([xi, yi, zi])[0]
except:
abort = True
return [0, 0, 0]
return [ex, ey, ez]
ax = plt.figure().add_subplot(projection='3d')
for q in Q:
dt = step_size
if q[3] < 0:
dt *= -1
for i in range(n_sphere):
phi = random.uniform(-np.pi, np.pi)
tet = random.uniform(-np.pi, np.pi)
lx = [q[0] + np.sin(phi) * np.cos(tet) * Rsphere]
ly = [q[1] + np.sin(phi) * np.sin(tet) * Rsphere]
lz = [q[2] + np.cos(phi) * Rsphere]
r = ode(IL3)
r.set_integrator(integrmodel)
r.set_initial_value([lx[0], ly[0], lz[0]], 0)
step = 0
abort = False
while r.successful():
step += 1
r.integrate(r.t+dt)
x, y, z = r.y[0], r.y[1], r.y[2]
lx.append(x)
ly.append(y)
lz.append(z)
go_out = False
for qf in Q:
if (x - qf[0])**2 + (y - qf[1])**2 + (z - qf[2])**2 < Rsphere2:
go_out = True
if go_out:
break
if s >= x or e <= x or s >= y or e <= y or s >= z or e <= z:
break
if step >= max_step:
break
if abort is True:
abort = False
break
if step >= max_step:
plt.plot(lx, ly, lz, 'r', lw=0.5)
else:
plt.plot(lx, ly, lz, 'k', lw=0.5)
for q in Q:
if q[3] > 0:
plt.plot(q[0], q[1], q[2], 'ro')
else:
plt.plot(q[0], q[1], q[2], 'bo')
ax.set_xlim(s, e)
ax.set_ylim(s, e)
ax.set_zlim(s, e)
plt.show()
Published: 2022-12-22 00:12:16