My Coding > Numerical simulations > Atoms and Molecules > Tools for molecular modelling > 2D random distribution with density function by Rejection Sampling techniques

2D random distribution with density function by Rejection Sampling techniques

In the previous example, I've explained how to generate random distribution for N-dots in the one-dimensional case in the presence of the density function. This was a very simple algorithm, but unfortunately, it was not suitable for multidimensional space. In this example, I will show how to solve this problem in a 2D case. And also, this 2D case can be extended to any dimension. Explanation with coding I've shown in the video.

2D distributions
2D distributions
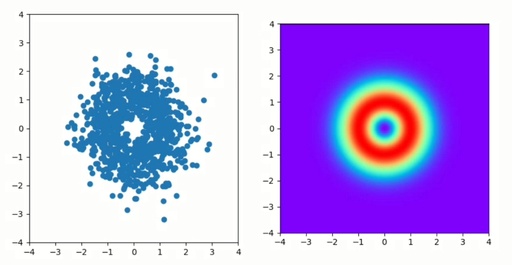
Comparison of generated random distribution of 1000 dots (left) with the density function used as a pattern (right).
Original image: 1073 x 555

Rejection Sampling techniques

What is the idea of rejection sampling? It is very easy. We generate a random dot in the given space and then we calculate the probability, or density in this spot, according to our function.

Probability function

The probability, or density function should be scaled to the same value as a later random threshold. To make everything easier, it is better to scale everything to 1.


def F(x, y):
    r = (x**2 + y**2)**0.5
    y = r**2 * np.exp(- r**2) / 0.3679
    return y

In this example, my function calculates random distribution (or density) with maximal value = 1.

Random sampling

In the next step, we generate a random dot in our range in the multidimensional space.


x = np.random.uniform(Xmin, Xmax)
y = np.random.uniform(Ymin, Ymax)
P = F(x, y)

And now, we need to make a random test for this dot. We need to generate random values in the same range and compare it with calculated probability. If the calculated probability is bigger than this random value, then we will accept this sample. Otherwise, we will reject it. 


threshold = np.random.uniform(0, 1)
if threshold < P:
    # Accept this sample

This is an idea of this method. Now you can watch the full video to see how to write the full code and display the results.

Full code for Rejection Sampling technique

This is a full code for the Rejection Sampling technique with some examples of visual representation


import numpy as np
import matplotlib.pyplot as plt

def F(x, y):
    r = (x**2 + y**2)**0.5
    y = r**2 * np.exp(- r**2) / 0.3679
    return y

N = 1000
Xmin, Xmax = -4, 4
Ymin, Ymax = -4, 4

points = [[], []]

while len(points[0]) < N:
    x = np.random.uniform(Xmin, Xmax)
    y = np.random.uniform(Ymin, Ymax)
    P = F(x, y)
    threshold = np.random.uniform(0, 1)

    if threshold < P:
        points[0].append(x)
        points[1].append(y)

xv = np.linspace(Xmin, Xmax, 200)
yv = np.linspace(Ymin, Ymax, 200)
x_grid, y_grid = np.meshgrid(xv, yv)

plt.figure(figsize=(10, 5))

plt.subplot(1,2,1)
plt.scatter(points[0], points[1])
plt.xlim(Xmin, Xmax)
plt.ylim(Ymin, Ymax)

plt.subplot(1,2,2)
plt.imshow(F(x_grid, y_grid), extent=[Xmin, Xmax, Ymin, Ymax], cmap='rainbow')

plt.show()

As you can see, we've calculated the density distribution for electrons in 2D space. In the next step, I will show you how to apply this code for the 3D case and how to visualise results for an electron cloud in the hydrogen atom.

I think for a full understanding of this code, you also need to look into my lecture about meshgrid.


Published: 2023-08-13 01:48:24

Last 10 artitles


9 popular artitles
© 2020 MyCoding.uk -My blog about coding and further learning. This blog was writen with pure Perl and front-end output was performed with TemplateToolkit.